The OPERA faster-than-light-neutrinos has become a bit of an obsession. But I have made a little progress.
1. I believe (and the last link in my previous note agrees) that it is the leading (and trailing) edge of the pulse that carries most of the timing information.
2. Here are the four leading and trailing edges from Extractions 1 & 2, from the OPERA paper.
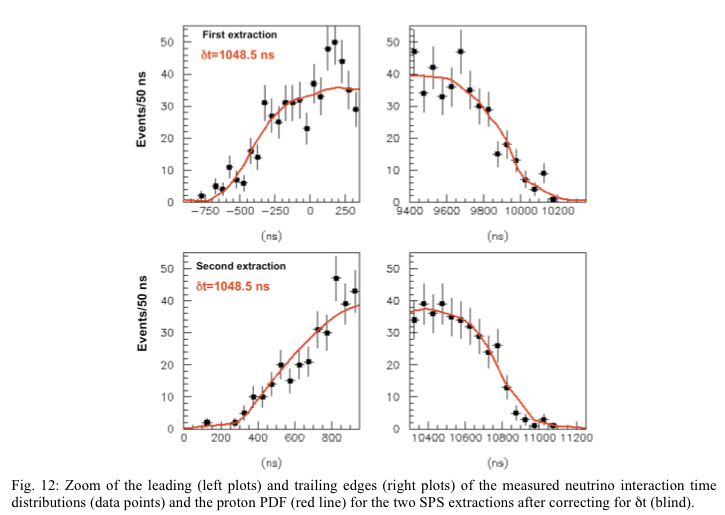
3. One can open the PDF paper in Photoshop, zoom in till it starts pixelating, and measure x,y coordinates on the diagram with the "Info" window. One measures the x,y coordinates along the axes for calibration, and then along the red proton curve and for the neutrino points, puts it all in a spreadsheet, and reconstruct the original curve. My spreadsheet is downloadable here. In it I have the reconstructed the leading edge of the First extraction, i.e., the upper left of Fig. 12 from diagram above.
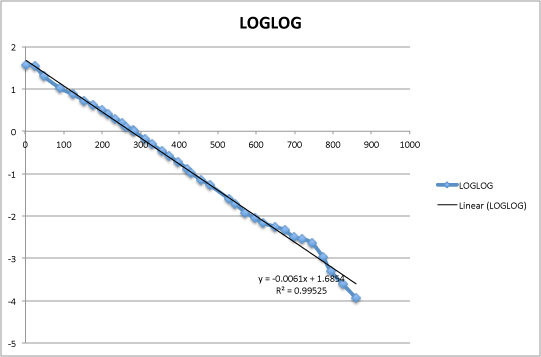
4. One wonders what kind of curve is the red proton curve? Just by eyeballing, taking logs, etc., I have found that the curve is very well approximated as
The log-log curve is shown here, with four of the points removed, that correspond to the leading tail.
1. I believe (and the last link in my previous note agrees) that it is the leading (and trailing) edge of the pulse that carries most of the timing information.
2. Here are the four leading and trailing edges from Extractions 1 & 2, from the OPERA paper.

3. One can open the PDF paper in Photoshop, zoom in till it starts pixelating, and measure x,y coordinates on the diagram with the "Info" window. One measures the x,y coordinates along the axes for calibration, and then along the red proton curve and for the neutrino points, puts it all in a spreadsheet, and reconstruct the original curve. My spreadsheet is downloadable here. In it I have the reconstructed the leading edge of the First extraction, i.e., the upper left of Fig. 12 from diagram above.
4. One wonders what kind of curve is the red proton curve? Just by eyeballing, taking logs, etc., I have found that the curve is very well approximated as
y = c * exp( - exp( -a * x + b ))
The log-log curve is shown here, with four of the points removed, that correspond to the leading tail.

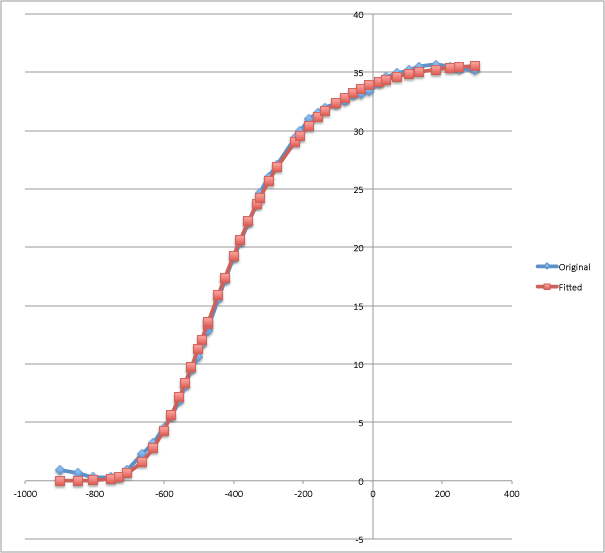
Superposing the original curve and the fitted one, I get this (purely eyeballing and experimenting).
5. I wonder whether there is a theoretical basis for the form of curve I found for the proton pulse.
The inner exponential is probably the response of a L-R circuit to a square pulse; so, e.,g it could be a magnetic field turning on. It is the physical origin of the outer exponential that is unclear to me - does the proton current turn on exponentially as the magnetic field turns on?
6. With that form of curve, I may perhaps do a least-squares fit to the proton curve and also see how well the neutrino points fit; and have a good estimate of the error. If I find anything interesting, then I'll have to digitize the other three curves and see what ensues.
The OPERA experiment has a standard error of around 10ns, and the effect they find is about 60ns, i.e., a 6-sigma result is claimed.
PS:
7. I neglected to put it up, but my eyeball fit is y=exp(3.58)* exp( - exp( -0.0061*x - 2.9201)).
(The x coordinate is time).
8. On the right side, the dying side of the pulse, the L-R circuit and magnetic field are decaying (for t > b) as exp(-a * (t - b)), and the proton pulse should die like c * (1 - exp( exp(- a* (t - b) ) ). I think I have that right. The problem with this interpretation is that in 7., my magnetic field turns on at x=-479, rather than -800 or so.)
Tomorrow is another day, maybe I will find the time to do a more calculated and less eye-ball fit.