What I'm trying to do with curve-fitting is to convince myself that the following is plausible, or figure out that it is not.
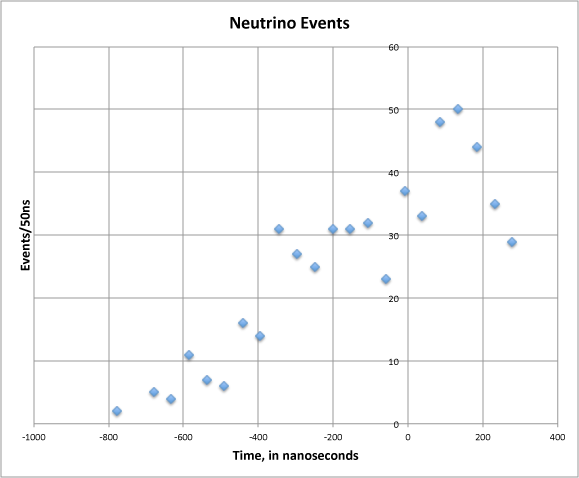
You are told that this is a (very sparse) sample of the leading edge of a pulse - it is going to plateau off at around 50 events/50ns beyond 400 ns for the next 9000ns or so) and that you want to fix the time of some feature of this pulse (its start, or the position of maximum slope, or position of half-peak-height, or some such) - to within 10 nanoseconds.
Suppose you're given the trailing edge, too, in a very similar form.
Next, you are told that this pulse is probably directly proportional to the following curve, time-shifted by some unknown amount.
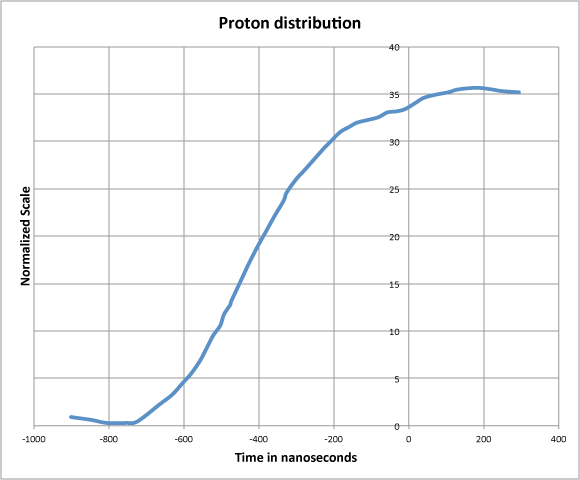
This second curve is the shape of the proton current averaged over a million pulses, that was used to generate neutrinos at CERN. The turning on of the current serves as a definite time marker for this curve. Neutrinos are generated at each instant at the target at CERN proportional to the height of this curve, and travel in an unknown time to the OPERA detector under the Gran Sasso mountain. There, some miniscule fraction are detected (the first set of points). Of course, you can synchronize clocks between the two sites, recording the exact when you detected each neutrino. You don't have corresponding time label on the proton, though, all you know is which one of the million pulses it was in.
You are able to fix the position of the bunch of points to within 10 nanoseconds, and also determine how much you have to shift the second curve for the best fit. You then account for all the delays in detector, electronics, etc., and remove that from the time-shift. What you're left with is the time of flight delay from CERN to Gran Sasso, which turns out to be shorter, by 60 nanoseconds, than the computed time of flight of light. (You can't use a light beam to directly measure the time of flight of light because the neutrino path is through 730 kilometers of rock).
You are told that this is a (very sparse) sample of the leading edge of a pulse - it is going to plateau off at around 50 events/50ns beyond 400 ns for the next 9000ns or so) and that you want to fix the time of some feature of this pulse (its start, or the position of maximum slope, or position of half-peak-height, or some such) - to within 10 nanoseconds.
Suppose you're given the trailing edge, too, in a very similar form.
Next, you are told that this pulse is probably directly proportional to the following curve, time-shifted by some unknown amount.

This second curve is the shape of the proton current averaged over a million pulses, that was used to generate neutrinos at CERN. The turning on of the current serves as a definite time marker for this curve. Neutrinos are generated at each instant at the target at CERN proportional to the height of this curve, and travel in an unknown time to the OPERA detector under the Gran Sasso mountain. There, some miniscule fraction are detected (the first set of points). Of course, you can synchronize clocks between the two sites, recording the exact when you detected each neutrino. You don't have corresponding time label on the proton, though, all you know is which one of the million pulses it was in.
You are able to fix the position of the bunch of points to within 10 nanoseconds, and also determine how much you have to shift the second curve for the best fit. You then account for all the delays in detector, electronics, etc., and remove that from the time-shift. What you're left with is the time of flight delay from CERN to Gran Sasso, which turns out to be shorter, by 60 nanoseconds, than the computed time of flight of light. (You can't use a light beam to directly measure the time of flight of light because the neutrino path is through 730 kilometers of rock).