The puzzler was that in a sample of some 118K tremblors of magnitude 4 or greater over a 10 year period, they occur more often on Thursdays and Sundays than any other day of the week. There is no physical or measurement bias reason for this to happen. We naively expect the number of earthquakes on any day of the week in this sample to be the same. Of course, as with any sample of random events, there won't be exactly the same number of events on each day of the week. But in this case, the deviation from the average is much larger than can be (naively) expected by chance.
Imagine tossing a fair coin 10 times. Fairly often, you will get 7 heads and 3 tails (or 3 heads and 7 tails), and not be surprised (roughly 12% of the time, each). If you toss the coin 100 times though, you expect to find 70 heads and 30 tails very rarely. The expectation is that the results will be centered around 50-50 (e.g., 55-45, 53-47, etc.)
But suppose the coin, while fair, has a memory. Suppose the probability of getting heads on a toss, **given that the previous toss gave a heads** is not 1/2 but 1/2 plus something (and likewise for tails, the next toss after a tails is somewhat more likely to be a tails). Can such a coin still be fair? Certainly. Systems in the real world often a finite memory, so eventually it will be true that the probability of a toss giving heads given that N tosses ago was heads will be 1/2, where N is some number, perhaps large. If the memory effect works exactly the same for tails as for heads, a little bit of reflection will suffice to convince yourself that in the long run this coin will yield as many tails as heads.
But see what happens: suppose the coin has an effective memory of 10 tosses. Then (in a handwaving way) a sequence of 100 tosses of the coin really corresponds to 10 **independent** tosses of the coin. And for a sequence of ten tosses, you aren't surprised when you get 70% heads and 30% tails, it happens quite often by pure chance.
The random processes that produces earthquakes also has a memory. This is what the autocorrelation function reveals.
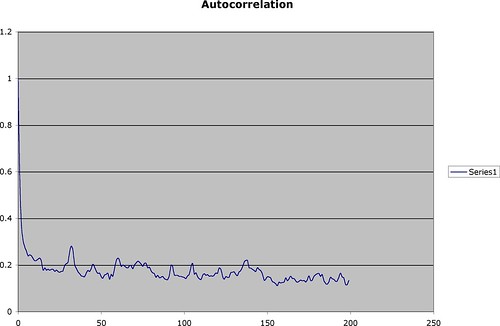What the chart is saying is that the underlying process has probabilities affected at a 15% level by events that happened 200 days ago. (I haven't displayed it here, but this extends out even to more than a year out). So, while the sample of earthquakes appears to be large - 118K earthquakes over 3650 days - in reality, just like the coin with the memory, there are much fewer **independent** instances, and we should not be surprised by seemingly large deviations from the average. In the comments on Prof. Rabett's blog, you will find that the predominance of Sunday earthquakes persists even with an additional decade of data. You will also find that if the week had 9 days instead of 7, the same weirdness would be there - one of the days of the 9 day week seems to be favored more than what (naive) chance would suggest.
