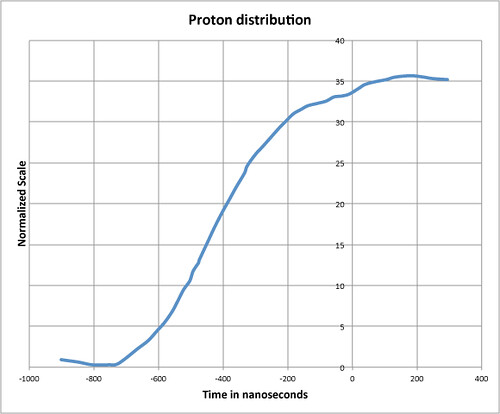
Readers of this blog may have noticed that ever since the OPERA collaboration announced finding neutrinos that travel faster than light, I have been scratching my head about something. Here, in the simplest possible terms is what I'm thinking about.
I’m pursuing a signal processing problem, not a physics problem. So, I’ll omit all of the physics.
Imagine a source emits a signal like the following.

The horizontal axis is time in nanoseconds.
The vertical axis is the intensity of the signal in arbitrary units.
The signal travels a precisely measured distance (731278.0 ± 0.2 meters), where it encounters a detector.
Here, a brief physics note is needed. Since the original signal has been transmuted along the way from electrically charged protons into electrically neutral, weakly interacting neutrinos, it is not possible to measure the signal in the same way as it was measured at the source. The detector instead detects a discrete set of events, the rate of events at its peak is about 1 event per nanosecond. (Overall, some 8000 events are detected.)
It is stipulated that the signal has not spread at all, and is in exactly the same shape at the detector. It is stipulated that the rate of detecting events is on the average proportional to the signal intensity. It is stipulated that the original signal, and all of the detected events at the detector are timed very precisely, with a root mean squared error of about 7.4 nanoseconds or better.
To measure the time of flight of the signal, it is necessary to precisely place a time-delayed version of the signal with respect to the detected events. I've tried to crudely depict that below. The little blue x's are the detected events marked on the time axis. The signal is shown with two different time delays below it. One "fits" the detected events better than the other.

The OPERA claim is that they can place the original signal on top of the detected events with a standard error of 6.9 nanoseconds. Moreover, as it turns out, the resulting time of flight is less than that of an equivalent light signal by 60.7 nanoseconds.
I believe that the underlying problem of measuring a time delay is one of edge detection. While there are "features" in the signal, the two crucial edges are the leading and trailing edge of the signal, and that is where about 10% of the overall detected events lie. Or to put it another way, here are neutrino events at one edge, binned in (number of events per 50 nanoseconds). Can you imagine placing the edge of the signal here with the claimed precision? It may be possible, but I need to convince myself of it.
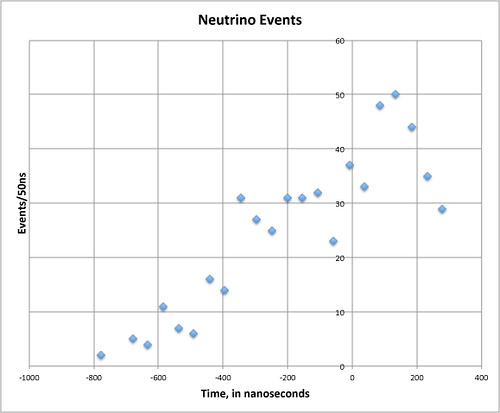
PS: on the same scale, the edge looks like this:I’m pursuing a signal processing problem, not a physics problem. So, I’ll omit all of the physics.
Imagine a source emits a signal like the following.

The horizontal axis is time in nanoseconds.
The vertical axis is the intensity of the signal in arbitrary units.
The signal travels a precisely measured distance (731278.0 ± 0.2 meters), where it encounters a detector.
Here, a brief physics note is needed. Since the original signal has been transmuted along the way from electrically charged protons into electrically neutral, weakly interacting neutrinos, it is not possible to measure the signal in the same way as it was measured at the source. The detector instead detects a discrete set of events, the rate of events at its peak is about 1 event per nanosecond. (Overall, some 8000 events are detected.)
It is stipulated that the signal has not spread at all, and is in exactly the same shape at the detector. It is stipulated that the rate of detecting events is on the average proportional to the signal intensity. It is stipulated that the original signal, and all of the detected events at the detector are timed very precisely, with a root mean squared error of about 7.4 nanoseconds or better.
To measure the time of flight of the signal, it is necessary to precisely place a time-delayed version of the signal with respect to the detected events. I've tried to crudely depict that below. The little blue x's are the detected events marked on the time axis. The signal is shown with two different time delays below it. One "fits" the detected events better than the other.

The OPERA claim is that they can place the original signal on top of the detected events with a standard error of 6.9 nanoseconds. Moreover, as it turns out, the resulting time of flight is less than that of an equivalent light signal by 60.7 nanoseconds.
I believe that the underlying problem of measuring a time delay is one of edge detection. While there are "features" in the signal, the two crucial edges are the leading and trailing edge of the signal, and that is where about 10% of the overall detected events lie. Or to put it another way, here are neutrino events at one edge, binned in (number of events per 50 nanoseconds). Can you imagine placing the edge of the signal here with the claimed precision? It may be possible, but I need to convince myself of it.